In der Debatte über PCR Testen hab ich bisher in der Öffentlichkeit wenige bzw. niemand gesehen, der den Satz von Bayes erwähnt hat, um die effektive Nützlichkeit des PCR Tests zu schätzen - obwohl der Satz von Bayes zum Grundwissen der Wahrscheinlichkeitslehre gehört.
Das Ergebnis ist NICHT intuitiv, siehe unten. Verzeiht bitte die Länge - ich habe es so kurz wie möglich gehalten, ohne daß es unklar bzw. mißverstanden werden könnte. Hab mein Bestes geleistet - Korrekturen aber gerne.
Man kann zeigen (Beweis ganz unten), daß:
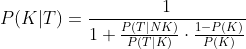
Wo:
K: krank
NK: nicht krank
T: positiver Test
P(...) sind "Chancen" d.h. Wahrscheinlichkeiten, d.h. Nummern von 0.0 bis 1.0 (1.0 entspricht 100%).
Eingangswerte (rechts vom "="):
P(K): Chancen, krank zu sein, d.h. kranker Anteil der gesamten Bevölkerung
P(T|NK): ich weiß, daß ich *nicht* krank bin (NK), und lasse mich testen. Wieviele Chancen hat der Test, positiv zu sein (T)? (heißt "false positive" in der wiss. Literatur).
P(T|K): ich weiß, daß ich krank bin (K), und lasse mich testen. Wieviele Chancen hat der Test, positiv zu sein (T)? (heißt "true positive" in der wiss. Literatur).
Ausgangswert (links vom "="):
P(K|T): ich lasse mich testen, und der Test ist positiv (T). Wieviele Chancen habe ich, krank zu sein (K)?
Soviel zum exakten Teil.
Der Ausgangswert ist der nützliche Wert in der Praxis, den man jetzt schätzen möchte.
Nur der Herrgott weiß die exakten Eingangswerte. Man kann aber anhand grober Eingangswerte eine Größeordnung vom Ausgangswert P(K|T) berechnen.
Nach https://www.medrxiv.org/content/10.1101/2020.04.16.20066787v2
P(T|K)=75/100 (d.h. 25% false negatives)Nach https://www.icd10monitor.com/false-positives-in-pcr-tests-for-covid-19
P(T|NK)=0.5/100 (d.h. 0.5% false positives)Nach https://grippeweb.rki.de/ (Stand 18.12.2020) probieren wir 3 unterschiedliche Größenordnungswerte für den kranken Anteil der gesamten deutschen Bevölkerung:
P(K)=3.1/100 "Regierungstreu", d.h. "alle mit akuter Atemwegserkrankung leiden an COVID-19".
Detail: wir schätzen diesen Wert als gleich mit der vom RKI gemeldeten Anzahl von Allen mit einer neu aufgetretenen akuten Atemwegserkrankung (ARE, mit Fieber oder ohne Fieber), den man auch auf der schwarzen Linie sieht, in KW50, in der Grafik unten (kopiert aus grippeweb.rki.de):
- "neu" hier kein Problem, wenn man annimmt, daß die Genesungsgeschwindigkeit etwa konstant bleibt - wie gesagt, es handelt sich hier nur um eine Größenordnungsschätzung, nicht um einen exakten Wert.
P(K)=1/100 "neutral", d.h. es gibt die noch, die Grippe ohne COVID-19.
P(K)=0.1/100 "Coronaleugner", d.h. "sehr wenige sind krank".
Beispielberechnung mit P(K)=3,1/100:
Ergebnisse für den Ausgangswert:
Siehe auch: https://www.icd10monitor.com/false-positives-in-pcr-tests-for-covid-19P(K)=3.1/100 "Regierungstreu" => ergibt: P(K|T)=82,8% d.h. obwohl der Test an sich im positiven Fall 99,5% zuverlässig sein soll, ist er in der Praxis nur 82,8% zuverlässig. Das ist so wegen dem etwa niedrigen P(K) Wert. Das meinte ich mit dem "nicht intuitiven Ergebnis".
P(K)=1/100 "neutral" => ergibt: P(K|T)=60,2% - der Test sieht langsam pfutsch aus. Man könnte auch eine Münze werfen (50%), es täte weniger weh. Hier kann man das "nicht intuitive Ergebnis" noch besser sehen.
P(K)=0.1/100 "Coronaleugner" => ergibt: P(K|T)=13,1% - muß man sich 6-7 mal testen lassen? Oder sollte man eher seinen Hund testen lassen?
Bei einem Test, der etwa 40 € kostet, werden gerade Unsummen in einen Vorgang, der selbst aus rein mathematischer Sicht sich für Diagnostik NICHT eignet. Nur wenn man schon Symptome hat (K), sollte man den Test nützen (P(T|K)=75/100). Alles Andere sinnfrei.
(Nebenbei: handelt es sich da nicht um etwa Bezahlung ohne nennenswerte Leistung, d.h. höflich gesagt "Vermögenstransfer"?)
Man könnte diese Unsummen woanders nützen: Bessere, effizientere und menschlichere Behandlung von Alten und Vorerkranken, die jetzt an COVID-19 leiden. (Dann dafür auch die Wirtschaft zum großen Teil laufen lassen.)
Systematische Untersuchung von positiven und negativen Korrelationen zwischen COVID-19 Fälle und regional bzw. persönlich unterschiedlichen Faktoren, anhand der Daten, die über 2020 akkumuliert wurden - und das am Besten länderübergreifend:
Anhand der gefundenen Korrelationen - schon da könnte man sich auf Überraschungen vorbereiten - die biologische Forschung präzis steuern.
Der medizinischer Forscher Claude Bernard hat schon im 19. Jahrhundert davor gewarnt, die Statistik auf einen Podest zu setzen. Die statistischen Ergebnisse sind nur da, um Hinweise zu geben, und damit die tatsächliche Forschung zu orientieren - die Statistik ersetzt aber keine echten biologischen und medizinischen Beweise.
Soeben gesehen:
Zusammenfassung: Ein Consortium von 22 Wissenschaftler mit Spezialisierung in Mikrobiologie, Virologie, Molekulargenetik und Molekularbiologie, Immunologie, Pharmacologie und andere Wissenschaftsbereiche fand "schwere Fehler" im Entwurf und Methodologie vom RT-PCR Test, die "den SARS-CoV2-PCR Test nützlos machen".
Es handelt sich um diesen Artikel: “Detection of 2019 novel coronavirus (2019-nCoV) by real-time RT-PCR,” von Victor Corman, leitendem Forscher Christian Drosten und 22 anderen Wissenschaflter, der am 21.01.2020 von Eurosurveillance empfangen wurde, und 2 Tage später (!) veröffentlicht wurde. Von ernsthafter Peer Review kann nicht die Rede sein.
Zusätzlich schauen wir hier den Anteil positiv getesteten, Positivenquote gennant:
Wir können diesen Wert 11,5% als P(T) nützen, und damit den Anteil Kranken P(K) schätzen, siehe Details in http://glat.info/pcrt/draft2 — Ergebnis: P(K)=15%, das wären eine Person von 6! Entspricht den grippeweb.rki.de ARE Werte nicht.
Nach Bestem Willen und Gewissen kann man den einen Verdächtigen Wert "false positives" P(T|NK) korrigieren, und zwar von 0.5% auf 10%, und damit realistischere Ergebnisse bekommen: P(K)=2% (eine kranke Person von 50), und leider Testzuverlässigkeit P(K|T)=13%. Details in http://glat.info/pcrt/draft2
Selbst ohne Mathe kann man direkt an den ganz offiziellen Statistiken eine Abkoppelung sehen, und zwar zwischen Positivenquote:
und akut Kranken (ARE, schwarze Linie) — beachtet bitte die unterschiedlichen Zeitskala:
Die einzige feststellbare Koppelung wäre zwischen Positivenquote und COVID-19-Rate, IfSG (rote Linie). Nun spricht der Ratio zwischen Positivenquote (gerade jetzt 11,69%) und COVID-19-Rate (gerade jetzt 0,2%) nicht für die zuverlässigkeit des PCR Tests: 11,69 / 0,2 = 69 !
Fast genau ein Jahr nach der Erscheinung vom RT-PCR Artikel von Drosten, interessiert sich das WHO doch auch für den Satz von Bayes:
WHO reminds IVD users that disease prevalence alters the predictive value of test results; as disease prevalence decreases, the risk of false positive increases (2). This means that the probability that a person who has a positive result (SARS-CoV-2 detected) is truly infected with SARS-CoV-2 decreases as prevalence decreases, irrespective of the claimed specificity.
Quelle: https://www.who.int/news/item/20-01-2021-who-information-notice-for-ivd-users-2020-05
Ähnlich wie der Satz von Bayes https://de.wikipedia.org/wiki/Satz_von_Bayes
Da das mathematische Ergebnis nicht intuitiv ist, kann man mit einer einfachen Monte-Carlo Simulierung prüfen, daß es keinen groben Fehler gibt.
Beispielimplementierung unten in JavaScript, kann in egal welchem Internet Browser (Firefox, Chrome usw.) ausgeführt werden. Einfach die JavaScript Konsole aufmachen, den Code unten kopieren:
und danach den folgenden Aufruf dazu in die JavaScript Konsole hineinschreiben:
test_all_three_scenarii()
Wegen der zufälligen Natur des Monte-Carlo Tests kommen jedes mal andere Werte heraus, dennoch sehr nah an den berechneten Werten. Z.B. bekam ich:
P(K): 3.1% => P(K|T): 82.8% P(K): 1.0% => P(K|T): 60.4% P(K): 0.1% => P(K|T): 13.3%