Position the ramp of a construction site by solving a quartic equation

by Guillaume Lathoud, February 2013

Problem

Result

Details

Below, the problem is described geometrically in the horizontal plane, turned into a 4th power polynomial equation, of which a direct, general solution is known since the Renaissance works of Ferrari (and Vieta).

Files are then shortly described, which implement this general solution.

Problem

The goal is to determine the position of blue ramp going down from the top of the red slopes to their bottom (all three are rectangles).

Both steep red slopes have the same \( depth\) and \(slope_{red}\), thus the same projected «horizontal width»: \[ qq_{red}~\buildrel\triangle\over =~ \frac{depth}{slope_{red}} \] where for example \(slope_{red} = tan(\pi\frac{60}{180})\) (60-degree red slopes).

The blue ramp has a given \(width_{blue}\) and a given \( slope_{blue}\), and thus a projected «horizontal length»: \[ horizlength_{blue}~\buildrel\triangle\over =~\frac{depth}{slope_{blue}} \] where \(slope_{blue} < slope_{red} \), for example \(slope_{blue} = 0.25 ~~(25\%)\).

Problem, projected onto the horizontal plane

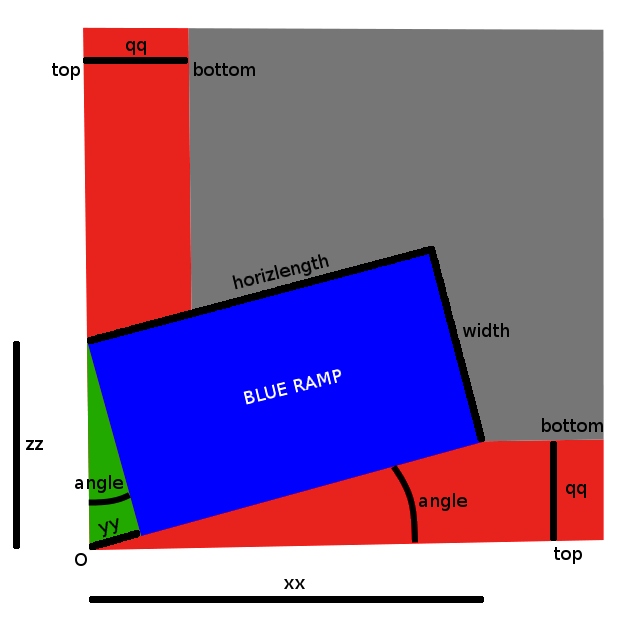
Constraints

The green triangle is horizontal. The leftmost corner of the blue ramp \(i \cdot zz\) must be at the top of the red slope.

The origin \(O\), the nearby corner of the blue ramp \( yy \cdot exp(i \cdot angle) \), and the rightmost corner of the blue ramp \( xx + i \cdot qq \) must be colinear. The latter must also be at the bottom of the red slope.

The problem is fully determined by \(qq\), \(horizlength\) and \(width\). To find the position of the blue ramp, we need to determine \(xx\), \(yy\), \(zz\) and \(angle\).

Equation

Since the ramp is rectangular, \( angle \) appears at several locations. Expressing for example \(tan(angle)\), one can show that: \[ qq \cdot width=xx \cdot yy \] Squaring both sides and using the Pythagorean theorem to express \(xx^2\), one obtains: \[ f(yy)=0 \] where: \[ f(yy)~\buildrel\triangle\over =~yy^2 \cdot ((horizlength+yy)^2-qq^2)-qq^2 \cdot width^2 \] which is a 4th power polynomial in \( yy \). The other variables \(xx\), \(zz\) and \(angle\) can all be derived from \( yy \).

Direct solution

Fortunately, the 4th power is the highest degree that can be algebraically solved [1][2] using a direct, general solution, which I decided to implement, so as to have reusable code. I chose Ferrari's solution [3], including Vieta's substitution in the depressed cubic case [4].

Files

Code I wrote to solve the problem:

• log.js and complex.js: Base code.
• solve_quartic.js: General solution of the quartic equation.
• solve_problem.js: Application to the specific ramp problem.
• LICENSE.TXT: Apache 2.0 License.

Third-party software, used to render this article:

• three.js and three.min.js: 3D rendering engine.
• trackballcontrols.js: Extension to rotate the 3D model.
• MathJax.js: Mathematical formula rendering engine.

Acknowledgments

Thanks to Felix Schädler for the initial request, and to the authors of three.js and MathJax for their excellent softwares.

References

[1] http://en.wikipedia.org/wiki/Quartic_function#History

[2] http://en.wikipedia.org/wiki/Abel%E2%80%93Ruffini_theorem

[3] http://en.wikipedia.org/wiki/Quartic_function

[4] http://en.wikipedia.org/wiki/Cubic_equation#Vieta.27s_substitution

License

  This HTML page contains the mathematical description of a problem
  and its solution, an interactive numerical demo and 3D demo, and 
  links to the programs I wrote to implement the solution.


  Copyright 2013 Guillaume Lathoud
  
  Licensed under the Apache License, Version 2.0 (the "License");
  you may not use this file except in compliance with the License.
  You may obtain a copy of the License at
  
  http://www.apache.org/licenses/LICENSE-2.0
  
  Unless required by applicable law or agreed to in writing, software
  distributed under the License is distributed on an "AS IS" BASIS,
  WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
  See the License for the specific language governing permissions and
  limitations under the License.
  
  A copy of the Apache License Version 2.0 as of February 20th, 2013
  can be found in the file ./LICENSE.TXT

File ./LICENSE.TXT